题目内容
如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG，②BE=CG，③DF=DH，④BH=CF．其中正确的是________．
①②③④
分析：连接CD．欲证线段相等，就证它们所在的三角形全等．证明△DBE≌△DCG，△DCH≌△DAF．
解答：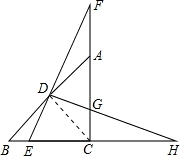
解：连接CD．
∵BD=AD=DC，CD⊥AB，∴∠BDE=∠CDG，∠DBE=∠DCE=45°
∴△DBE≌△DCG，∴DE=DG；BE=CG．
同理可证△DCH≌△DAF，∴DF=DH；AF=CH．
∵BC=AC，CH=AF，∴BH=CF．
故填：①②③④．
点评：本题重点考查了对三角形全等的判定定理和等腰直角三角形的理解和掌握，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS．
分析：连接CD．欲证线段相等，就证它们所在的三角形全等．证明△DBE≌△DCG，△DCH≌△DAF．
解答：
解：连接CD．∵BD=AD=DC，CD⊥AB，∴∠BDE=∠CDG，∠DBE=∠DCE=45°
∴△DBE≌△DCG，∴DE=DG；BE=CG．
同理可证△DCH≌△DAF，∴DF=DH；AF=CH．
∵BC=AC，CH=AF，∴BH=CF．
故填：①②③④．
点评：本题重点考查了对三角形全等的判定定理和等腰直角三角形的理解和掌握，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
12、如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG；②BE=CG；③DF=DH；④BH=CF．其中正确的是（ ）
18、如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG，②BE=CG，③DF=DH，④BH=CF．其中正确地是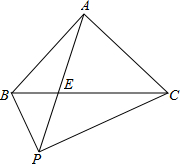
如图，P为等腰Rt△ABC外一点，∠BAC=90°，连PB、PC、PA，PA交BC于E点，且∠APC=45°，下列结论：
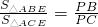．③PB+PC=
PA．