题目内容
如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG；②BE=CG；③DF=DH；④BH=CF．其中正确的是（ ）
| A．②③ | B．③④ | C．①④ | D．①②③④ |
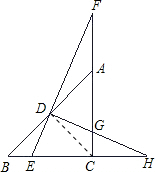
根据已知条件，
∵△ABC是等腰直角三角形，CD是中线．
∴BD=DC，∠B=∠DCA=45°．
又∵∠BDC=∠EDH=90°，即∠BDE+∠EDC=∠EDC+∠CDH
∴∠BDE=∠CDH
∴△DBE≌△DCG（ASA）
∴DE=DG；BE=CG．
同理可证：△DCH≌△DAF，可得：DF=DH；AF=CH．
∵BC=AC，CH=AF，∴BH=CF．
故选D．
练习册系列答案
相关题目
12、如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG；②BE=CG；③DF=DH；④BH=CF．其中正确的是（ ）
18、如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG，②BE=CG，③DF=DH，④BH=CF．其中正确地是
如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①DE=DG，②BE=CG，③DF=DH，④BH=CF．其中正确的是________．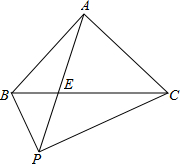
如图，P为等腰Rt△ABC外一点，∠BAC=90°，连PB、PC、PA，PA交BC于E点，且∠APC=45°，下列结论：
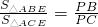．③PB+PC=
PA．