题目内容
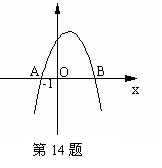
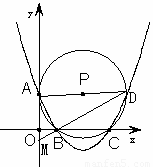
已知如图,抛物线 与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。

(1)请直接写出答案:点A坐标 ,⊙P的半径为 ;
(2)求抛物线的解析式;
(3)若 ,求N点坐标;
,求N点坐标;
(4)若△AOB与以A、B、D为顶点的三角形相似,求MB?MD的值.
(1)(0,2),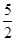 ;(2)
;(2)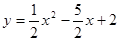 ;(3)(6,5);(4)
;(3)(6,5);(4)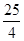 或
或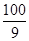
【解析】
试题分析:(1)根据抛物线与坐标轴的交点坐标的特征结合切线的性质求解即可;
(2)根据抛物线过B(1,0)、C(4,0),设y=a(x-1)(x-4),再把A(0,2)代入求即;
(3)设N点坐标为(x0,y0),由题意有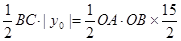 ,即可求得y0的值,再根据函数图象上的点的坐标的特征求解即可;
,即可求得y0的值,再根据函数图象上的点的坐标的特征求解即可;
(4)根据题意∠OAB=∠ADB,所以△AOB和△ABD相似有两种情况:①∠ABD和∠AOB对应,此时AD是⊙P的直径;②∠BAD和∠AOB对应,此时BD是⊙P的直径,所以直线MB过P点,分别根据相似三角形的性质求解即可.
(1)A点坐标是(0,2),⊙P的半径长为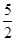 ;
;
(2)抛物线过B(1,0)、C(4,0),设y=a(x-1)(x-4)
将A(0,2)代入得4a=2,解得a=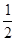
抛物线的解析式是: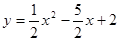 ;
;
(3)设N点坐标为(x0,y0),由题意有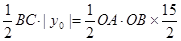
∴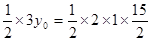 ,解得y0=5
,解得y0=5
∵N点在抛物线上
∴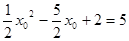
解得 x0=6或 x0=1(不合题意,舍去)
∴N点的坐标为(6,5);
(4)根据题意∠OAB=∠ADB,所以△AOB和△ABD相似有两种情况:
①∠ABD和∠AOB对应,此时AD是⊙P的直径
则AB=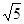 ,AD=5
,AD=5
∴ BD=2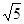
∵Rt△AMB∽Rt△DAB
∴ MA:AD=AB:BD 即 MA=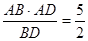
∵Rt△AMB∽Rt△DMA
∴MA:MD=MB:MA
即 MB·MD=MA2=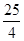
②∠BAD和∠AOB对应,此时BD是⊙P的直径,所以直线MB过P点
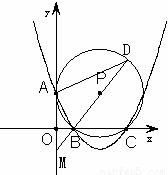
∵B(1,0),P(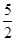 ,2)
,2)
∴直线MB的解析式是: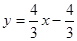
∴M点的坐标为(0,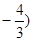
∴AM=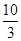
由△MAB∽△MDA得MA:MD=MB:MA
∴MB·MD=MA2=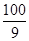 .
.
考点:二次函数的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
 与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
 ,求N点坐标;
,求N点坐标;