题目内容
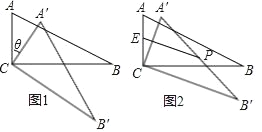
【题目】如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.

【答案】8
【解析】
连结EO并延长交CF于点H,证明四边形E B′CH是矩形,在Rt△OCH中,根据勾股定理得CH,代入数值求出CF=2CH =8.
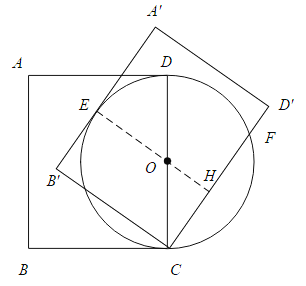
连结EO并延长交CF于点H,
∵矩形ABCD绕点C旋转得到矩形A′B′CD′,
∴∠B′=∠B′CD′=90°,A′B′∥CD′,BC=B′C=8
∵A′B′切⊙O与点E,
∴OE⊥A′B′,
∴四边形E B′CH是矩形,
∴EH= B′C=8,OH⊥CF
∵AB=10,
∴OE=OC =![]() AB=5,
AB=5,
∴OH=3,
在Rt△OCH中,根据勾股定理得![]() ,
,
∴CF=2CH =8.
故答案为:8.

练习册系列答案
相关题目