题目内容
. 如图1,已知正比例函数和反比例函数的图像都经过点M(-2,![]() ),且P(
),且P(![]() ,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
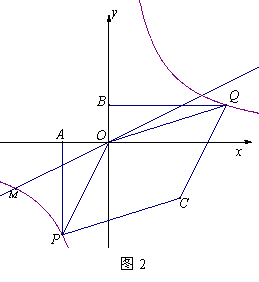
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
 | |||
 | |||
(1)设正比例函数解析式为![]() ,将点M(
,将点M(![]() ,
,![]() )坐标代入得
)坐标代入得![]() ,所以正比例函数解析式为
,所以正比例函数解析式为![]()
同样可得,反比例函数解析式为![]()
(2)当点Q在直线DO上运动时,
设点Q的坐标为![]() ,
,
于是![]() ,
,
而![]() ,
,
所以有,![]() ,解得
,解得![]()
所以点Q的坐标为![]() 和
和![]()
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,
而点P(![]() ,
,![]() )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
因为点Q在第一象限中双曲线上,所以可设点Q的坐标为![]() ,
,
由勾股定理可得![]() ,
,
所以当![]() 即
即![]() 时,
时,![]() 有最小值4,
有最小值4,
又因为OQ为正值,所以OQ与![]() 同时取得最小值,
同时取得最小值,
所以OQ有最小值2.
由勾股定理得OP=![]() ,所以平行四边形OPCQ周长的最小值是
,所以平行四边形OPCQ周长的最小值是
![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
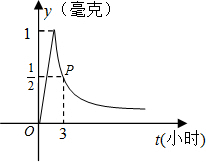 教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
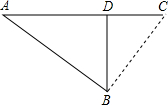
 日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为
日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为 要经过多少小时后,学生才能进入教室?
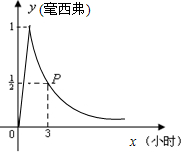
要经过多少小时后,学生才能进入教室? (2011•巴中)某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长BC=20m,斜坡上的影长CD=8m,已知斜坡CD与操场平面的夹角为30°,同时测得身高l.65m的学生在操场 上的影长为3.3m.求旗杆AB的高度.(结果精确到1m)
(2011•巴中)某校初三年级“数学兴趣小组”实地测量操场旗杆的高度.旗杆的影子落在操场和操场边的土坡上,如图所示,测得在操场上的影长BC=20m,斜坡上的影长CD=8m,已知斜坡CD与操场平面的夹角为30°,同时测得身高l.65m的学生在操场 上的影长为3.3m.求旗杆AB的高度.(结果精确到1m)