题目内容
如图,直线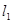 、
、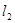 均被直线
均被直线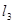 、
、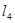 所截,且
所截,且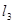 与
与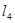 相交,给定以下三个条件:
相交,给定以下三个条件:
①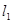 ⊥
⊥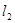 ;②∠1 =∠2;③∠2 +∠3=90°;
;②∠1 =∠2;③∠2 +∠3=90°;
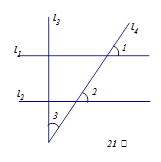
请从这三个条件中选择两个作为条件,另一个作为结论组成一个真命题,并进行证明,
已知:
求证:
证明:
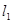 、
、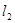 均被直线
均被直线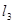 、
、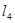 所截,且
所截,且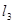 与
与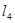 相交,给定以下三个条件:
相交,给定以下三个条件:①
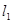 ⊥
⊥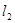 ;②∠1 =∠2;③∠2 +∠3=90°;
;②∠1 =∠2;③∠2 +∠3=90°;
请从这三个条件中选择两个作为条件,另一个作为结论组成一个真命题,并进行证明,
已知:
求证:
证明:
解:可以组成三个命题:
(1)已知: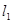 ⊥
⊥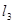 ,∠1 =∠2,求证:∠2 +∠3 = 90°;
,∠1 =∠2,求证:∠2 +∠3 = 90°;
(2)已知: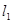 ⊥
⊥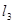 ,∠2 +∠3 = 90°,求证:∠1 =∠2;
,∠2 +∠3 = 90°,求证:∠1 =∠2;
(3)已知:∠2 +∠3 = 90°,∠1 =∠2,求证: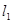 ⊥
⊥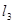 ;
;
证明略:
(1)已知:
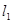 ⊥
⊥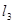 ,∠1 =∠2,求证:∠2 +∠3 = 90°;
,∠1 =∠2,求证:∠2 +∠3 = 90°;(2)已知:
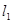 ⊥
⊥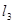 ,∠2 +∠3 = 90°,求证:∠1 =∠2;
,∠2 +∠3 = 90°,求证:∠1 =∠2;(3)已知:∠2 +∠3 = 90°,∠1 =∠2,求证:
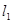 ⊥
⊥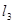 ;
;证明略:
如果选择①②两个作为条件,③作为结论可组成一个真命题.首先根据平行线的判定定理,可得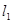 ∥
∥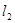 ,由
,由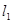 ⊥
⊥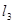 ,可得
,可得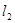 ⊥
⊥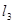 ,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.
,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.
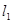 ∥
∥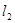 ,由
,由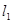 ⊥
⊥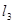 ,可得
,可得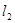 ⊥
⊥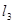 ,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.
,然后,根据直角三角形的两个锐角互余及对顶角的性质,即可证明.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


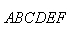 绕着中心
绕着中心 旋转角
旋转角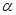 得到的图形与原来的图形重合,则
得到的图形与原来的图形重合,则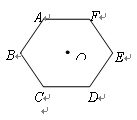




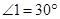 ,则
,则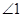 的补角的度数为 度.
的补角的度数为 度.