��Ŀ����
����Ŀ����֪��O����ABC�ڣ���֪OB��OC�ֱ�ƽ�֡�ABC�͡�ACB����O��ֱ��EF�ֱ�AB��AC��E��F��
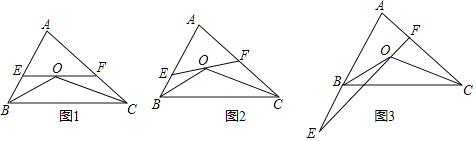
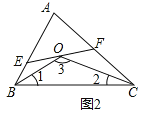
��1����ͼ1����֪EF��BC��
������A��76������ֱ��д����BOE+��COF�Ķ�����
�ڲ����BOE����COF���A֮����������������ϵ��д�����ۣ�����֤��
��2��ֱ��EF�Ƶ�O��ת����ͼ2��λ��ʱ��EF��BC��ƽ�У�����ô���棨1�����в���Ľ��ۻ���������������������֤�����������������˵�����ɣ�
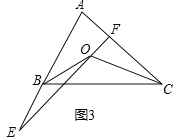
��3����ֱ��EF�Ƶ�O��ת����ͼ3��λ��ʱ����E��AB���ӳ����ϣ�����ֱ��д����BOE����COF���A֮���������ϵ��
���𰸡���1����52�����ڡ�BOE+��COF��90����![]() ��A�����ɼ���������2�����������ɼ���������3����COF����BOE��90����
��A�����ɼ���������2�����������ɼ���������3����COF����BOE��90����![]() ��A
��A
��������
��1���ٸ���ƽ���ߵ����ʺ��������ڽǺͶ������м��㣻
���â��еķ��������Ƶ���ͬ������ƽ���ߵ����ʺ��������ڽǺͶ����ó��ǵĹ�ϵ��
��2�������������ڽǺͶ����Լ�ƽ�ǵ����ʼ���֤�á�BOE+��COF=90��-![]() ��A��
��A��
��3�������������ڽǺͶ����Լ�ƽ�ǵĶ��弴��֤�á�COF-��BOE=90��-![]() ��A.
��A.
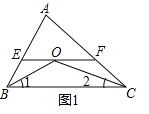
��1������ͼ1����EF��BC��
���BOE����1����COF����2��
��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB
��ACB
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A��
��A��
���BOE+��COF����1+��2��90����![]() ��A��90����
��A��90����![]() ��52����
��52����
�ڲ����BOE+��COF��90����![]() ��A��
��A��
֤������EF��BC��
���BOE����1����COF����2��
��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB
��ACB
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A��
��A��
���BOE+��COF����1+��2��90����![]() ��A��
��A��
��2��������
֤������ͼ2����OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB��
��ACB��
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A
��A
�ߡ�BOE+��COF+��3����1+��2+��3��180��
���BOE+��COF����1+��2��90����![]() ��A��
��A��
��3���⣺��ͼ3����OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���OBC��![]() ��ABC����OCB��
��ABC����OCB��![]() ��ACB��
��ACB��
���BOC��180����![]() ��ABC+
��ABC+![]() ��ACB��180����
��ACB��180����![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90��+
��180������A����90��+![]() ��A��
��A��
�ߡ�BOC����BOE+��COF��180����
���COF����BOE��180������BOC��180������90��+![]() ��A����90����
��A����90����![]() ��A��
��A��

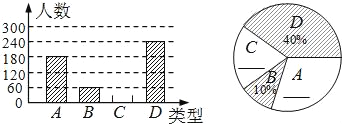
����Ŀ��������20�����ˣ�ij�������������������ͳ�����±���
����20������ijһ���������������ͳ�Ʊ�
��������ĸ��������� | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
�����������ˣ� | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ��������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������