题目内容
(2003•西城区模拟)清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步: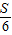 =m;第二步:
=m;第二步: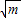 =k;第三步:分别用3、4、5乘k,得三边长”.
=k;第三步:分别用3、4、5乘k,得三边长”.(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗请写出证明过程.
【答案】分析:先由题中所给的条件找出字母所代表的关系,然后套用公式解题.
解答:解:(1)当S=150时,k=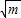 =
=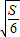 =
=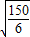 =
=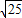 =5,
=5,
所以三边长分别为:3×5=15,4×5=20,5×5=25;
(2)证明:三边为3、4、5的整数倍,
设为k倍,则三边为3k,4k,5k,
而三角形为直角三角形且3k、4k为直角边.
其面积S= (3k)•(4k)=6k2,
(3k)•(4k)=6k2,
∴k2= ,k=
,k=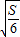 (k>0),
(k>0),
即:将面积除以6,然后开方,即可得到倍数.
点评:此题信息量较大,解答此类题目的关键是要找出所给条件,然后解答.
解答:解:(1)当S=150时,k=
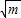 =
=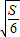 =
=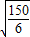 =
=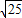 =5,
=5,所以三边长分别为:3×5=15,4×5=20,5×5=25;
(2)证明:三边为3、4、5的整数倍,
设为k倍,则三边为3k,4k,5k,
而三角形为直角三角形且3k、4k为直角边.
其面积S=
 (3k)•(4k)=6k2,
(3k)•(4k)=6k2,∴k2=
 ,k=
,k=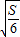 (k>0),
(k>0),即:将面积除以6,然后开方,即可得到倍数.
点评:此题信息量较大,解答此类题目的关键是要找出所给条件,然后解答.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目


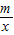 图象的一个交点为A(2,4),那么k= ,m= .
图象的一个交点为A(2,4),那么k= ,m= .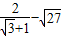 .
.