��Ŀ����
����Ŀ����ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B��PΪ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N��
��1������C�ڵ�һ����ʱ����֤����OPM�ա�PCN��
��2������C�ڵ�һ����ʱ����AP��Ϊm���ı���POBC�����ΪS�������S��m��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3������P���߶�AB���ƶ�ʱ����CҲ��֮��ֱ��x=1���ƶ�����PBC�Ƿ���ܳ�Ϊ���������Σ�������ܣ����������ʹ��PBC��Ϊ����ֱ�������εĵ�P�����ꣻ��������ܣ���˵�����ɡ�

���𰸡���1��֤����������
��2��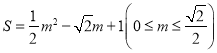
��3��ʹ��PBCΪ���������εĵĵ�P������Ϊ��0��1����![]() ,1��
,1��![]() ��
��
���������⣺��1����OM��BN��MN��OB����AOB=900��
�������ı���OBNMΪ���Ρ�
������MN=OB=1,��PMO=��CNP=900
������![]() ��AO=BO=1��
��AO=BO=1��
������AM=PM��
������OM=OA-AM=1-AM��PN=MN-PM=1-PM��
������OM=PN�������ߡ�OPC=900��
�������OPM+CPN=900��
�����֡ߡ�OPM+��POM=900�������CPN=��POM��
�������OPM�ա�PCN.������������������������������������������������
������2����AM=PM=APsin450= ![]() ��
��
������NC=PM= ![]() ����BN=OM=PN=1-
����BN=OM=PN=1- ![]() ��
��
������BC=BN-NC=1- ![]() -
- ![]() =
= ![]()
����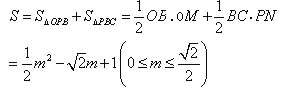
������3����PBC������������������������������������������������������
�����ٵ�P��A�غ�ʱ��PC=BC=1����ʱP��0��1��
�����ڵ���C�ڵ������ޣ���PB=CBʱ��
������BN=PN=1��![]() ��������BC=PB=
��������BC=PB=![]() PN=
PN=![]() -m��
-m��
��NC=BN+BC=1��![]() +
+![]() -m��
-m��
�����ɢ�֪��NC=PM= ![]() ��
��
������1��![]() +
+![]() -m=
-m= ![]() ��������m=1.������������������
��������m=1.������������������
������PM= ![]() =
=![]() ��BN=1��
��BN=1��![]() =1��
=1��![]() ��������P��
��������P��![]() ,1��
,1��![]() ��.
��.
��ʹ��PBCΪ���������εĵĵ�P������Ϊ��0��1����![]() ,1��
,1��![]() ����
����



