题目内容
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC. 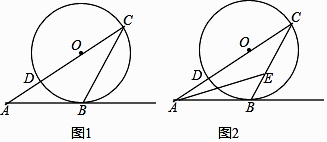
(1)如图1,若∠A=26°,求∠C的度数;
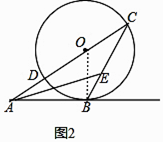
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.
【答案】
(1)解:连接OB,如图1,
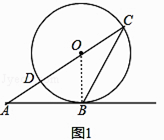
∵AB切⊙O于B,
∴∠ABO=90°,
∵∠A=26°,
∴∠AOB=90°﹣26°=64°,
∵OC=OB,
∴∠C=∠CBO,
∵∠AOB=∠C+∠CBO,
∴∠C= ![]() =32°
=32°
(2)解:连接OB,如图2,
∵AE平分∠BAC,
∴∠CAE= ![]() ∠CAB,
∠CAB,
∵由(1)知:∠OBE=90°,∠C=∠CBO,
又∵∠C+∠CAB+∠CBA=180°,
∴2∠C+2∠CAE=90°,
∴∠CAE+∠C=45°,
∴∠AEB=∠CAE+∠C=45°
【解析】(1)连接OB,根据切线性质求出∠ABO=90°,根据三角形内角和定理求出∠AOB,求出∠C=∠OBC,根据三角形外角性质求出即可;(2)根据三角形内角和定理求出2∠C+2∠CAE=90°,求出∠C+∠CAE=45°,根据三角形外角性质求出即可.
【考点精析】认真审题,首先需要了解三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角),还要掌握三角形的外角(三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.

练习册系列答案
相关题目