题目内容
【题目】完成下列小题
(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。 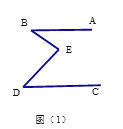
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系?请探索。 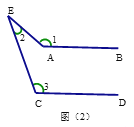
【答案】
(1)AB∥CD.在∠BED的内部作∠BEF=∠B, ∴AB∥EF. ∵∠B+∠D=∠BED, ∴∠BE F+∠FED=∠BED, ∴∠FED=∠D, ∴EF∥CD, ∴A B∥CD.
(2) 提示:以点E为顶点,EA为一边,作∠AEF与∠1互补,得EF∥AB,使∠FEC=∠3=180°,即180°-∠1+∠2+∠3=180°,∠2+∠3=∠1时,EF∥CD. ∵EF∥AB,EF∥CD, ∴AB∥CD.
【解析】(1)AB∥CD.在∠BED的内部作∠BEF=∠B, ∴AB∥EF. ∵∠B+∠D=∠BED,∴∠BE F+∠FED=∠BED, ∴∠FED=∠D, ∴EF∥CD, ∴A B∥CD.(2)提示:以点E为顶点,EA为一边,作∠AEF与∠1互补,得EF∥AB,使∠FEC=∠3=180°,即180°-∠1+∠2+∠3=180°,∠2+∠3=∠1时,EF∥CD. ∵EF∥AB,EF∥CD, ∴AB∥CD.
【考点精析】本题主要考查了平行线的判定的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能正确解答此题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目