题目内容
【题目】已知不在同一条直线上的三点P，M，N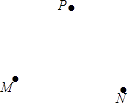 
（1）画射线NP；再画直线MP；
（2）连接MN并延长MN至点R，使NR=MN；（保留作图痕迹，不写作图过程）
（3）若∠PNR比∠PNM大100°，求∠PNR的度数．
【答案】
（1）解：射线NP、直线MP如图所示
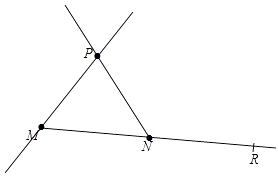
（2）解：连接MN并延长MN至点R，使NR=MN，点R即为舍弃（如图）
（3）解：∵∠PNR=∠PNM+100°，∠PNR+∠PNM=180°，
∴∠PNM+（∠PNM+100°）=180°，
∴2∠PNM=80°，
∴∠PNM=40°
【解析】（1）根据射线、直线的定义画出图形即可．（2）连接MN并延长MN至点R，截取NR=MN即可．（3）由题意可知∠PNR=∠PNM+100°，∠PNR+∠PNM=180°，即∠PNM+（∠PNM+100°）=180°，由此即可解决问题
练习册系列答案
相关题目
【题目】学校体育课进行定点投篮比赛，10位同学参加，每人连续投5次，投中情况统计如下：
投中球数量（个） | 2 | 3 | 4 | 5 |
人数（人） | 1 | 4 | 3 | 2 |
这10位同学投中球数量的众数和中位数分别是（ ）
A. 4, 2 B. 3，4 C. 2，3.5 D. 3，3.5
【题目】某景区在“春节”假期间，每天接待的游客人数统计如下：(单位：万人)
农历 | 十二月三十 | 正月初一 | 正月初二 | 正月初三 | 正月初四 | 正月初五 | 正月初六 |
人数 | 1.2 | 2.3 | 2 | 2.3 | 1.2 | 2.3 | 0.6 |
表中表示人数的一组数据中，众数和中位数分别是______和_______．
