题目内容
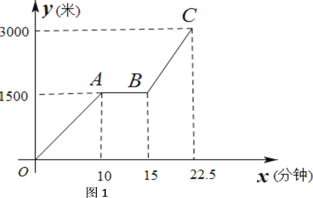
【题目】小李和小陆从 A 地出发，骑自行车沿同一条路行驶到 B 地，他们离出发地的距离 s和行驶时间t之间的关系的图象如图，根据图象回答下列问题：
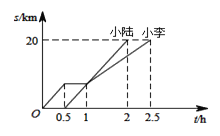
(1) 小李在途中逗留的时间为___________h，小陆从 A 地到 B 地的速度是________km/h；
(2) 当小李和小陆相遇时，他们离 B 地的路程是____________千米；
(3) 写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为_____________________.
【答案】（1）0.5，
； （2）；（3）
【解析】
试题（1）通过观察图象可得到距离没有发生变化的即为逗留的时间；用路程除以时间即可得出小陆的速度；
（2）根据速度一定，路程与时间成正比即可求解；
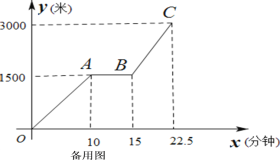
（3）如图，求出N点坐标，即可得出M点坐标，从而可求出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式.
试题解析：（）1如图所示，
线段MN说明小李在行驶过程中停留的时间为（1-0.5）=0.5小时．
小陆从 A 地到 B 地的速度是20÷（2-0.5）=
km/小时．
（2）20-×（1-0.5）=km;
(3)易知N（1， 
），所以M（0.5，）
设OM的函数关系式为s=kt
把M（0.5，）代入s=kt得：k=.
∴小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为
练习册系列答案
相关题目
