题目内容
【题目】如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
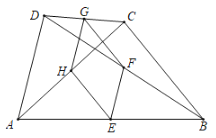
(1)求证:四边形EFGH是平行四边形;
(2)当AD⊥BC时,四边形EFGH是哪种特殊的平行四边形?
【答案】(1)见详解;(2)平行四边形EFGH是矩形,理由见详解
【解析】
(1)根据三角形中位线定理得到EF=![]() AD,EF∥AD,GH=
AD,EF∥AD,GH=![]() AD,GH∥AD,得到EF=GH,EF∥GH,根据平行四边形的判定定理证明;
AD,GH∥AD,得到EF=GH,EF∥GH,根据平行四边形的判定定理证明;
(2)根据有一个角是直角的平行四边形是矩形解答.
(1)证明:∵E、F分别是AB、BD的中点,
∴EF是△BAD的中位线,
∴EF=![]() AD,EF∥AD,
AD,EF∥AD,
同理,GH=![]() AD,GH∥AD,
AD,GH∥AD,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形;
(2)平行四边形EFGH是矩形,
理由如下:∵EF∥AD,
∴∠FEB=∠DAB,
∵EH∥BC,
∴∠HEA=∠ABC,
∵AD⊥BC,
∴∠DAB+∠ABC=90°,
∴∠HEF=90°,
∴平行四边形EFGH是矩形.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目