Question

（2013•绍兴模拟）小刚在纸上画了一个面积为6分米²的正六边形，然后连接相隔一点的两点得到如图所示的对称图案，他发现中间也出现了一个正六边形，则中间的正六边形的面积是

2

分米²．

Answer 1

分析：首先设O是原正六边形的中心，连接AO，FO，MO，设FO与AE交于点Q，AO与BE交于P，易得△OAF是等边三角形，继而可得点M是△AOF的外心，然后由一个面积为6分米²的正六边形，求得△OPM的面积，继而求得答案．

解答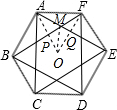：解：设O是原正六边形的中心，连接AO，FO，MO，设FO与AE交于点Q，AO与BE交于P，
∵一个面积为6分米²的正六边形，连接相隔一点的两顶点得到如图所示的对称图案，
∴∠AOF=

1

6

×360°=60°，S_△AOF=

1

6

×6=1（分米²），
∴△OAF是等边三角形，
∵AB=AF，
∴OA⊥BF，
∴AP=OP，
∴AM=OM，
同理：OF⊥AE，OQ=FQ，
∴OM=FM，
∴点M是△AOF的外心，
∴S_△OAM=

1

3

S_△AOF=

1

3

（分米²），
∴S_△OPM=

1

2

S_△OAM=

1

6

（分米²），
∴中间的正六边形的面积是：12×S_△OPM=2（分米²）．
故答案为：2．

点评：此题考查了圆与正多边形的性质．此题难度较大，注意掌握辅助线的作法是解此题的关键，注意数形结合思想的应用．