Question

（2013•绍兴模拟）将正方形ABCD的各边三等分（如图所示），连接各分点．现在正方形ABCD内随机取一点，则这点落在阴影部分的概率是（　　）

• A．

  1

  9

• B．

  1

  8

• C．

  1

  7

• D．

  1

  6

Answer 1

分析：根据题意，图中每个小阴影面积都相等，利用相似三角形的判定与性质得出

S△EFQ

S△DAO

=

1

9

，进而得出

阴影部分面积

正方形面积

=

1

9

，由几何概率的求法，可得答案．

解答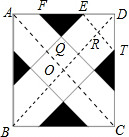：解：连接AC，BD，ET，ET交BD于点R，AC与BD交于点O，
∵将正方形ABCD的各边三等分（如图所示），连接各分点，
∴AF=EF=ED，ET∥AC，
根据题意得出△FEQ≌△EDR，
∵ET∥AC，
∴△DER∽△DAO，
∵

ED

AD

=

1

3

，
∴

S△DER

S△DAO

=

1

9

，
故

S△EFQ

S△DAO

=

1

9

，
同理可得：

阴影部分面积

正方形面积

=

1

9

，
故现在正方形ABCD内随机取一点，则这点落在阴影部分的概率是：

1

9

，
故选：A．

点评：本题考查了几何概率的求法以及正方形的性质、相似三角形的判定与性质等知识，注意结合概率的性质进行计算求解．用到的知识点为：概率=所求情况数与总情况数之比．