题目内容
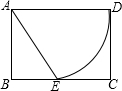
如图,已知矩形纸片ABCD,AD=2,AB=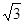 ,以A为圆心,AD长为半径画弧交BC于点E,将扇形AED剪下围成一个圆锥,则该圆锥的底面半径为 .
,以A为圆心,AD长为半径画弧交BC于点E,将扇形AED剪下围成一个圆锥,则该圆锥的底面半径为 .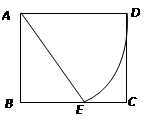
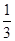
解析试题分析:由题意可得AE=AD=2,再根据勾股定理可求得BE=1,即可得到∠BAE的度数,从而得到∠DAE的度数,求得扇形的弧长即可得到圆锥的底面半径.
由题意得AE=AD=2,
则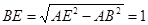
∴∠BAE=30°
∴∠DAE=60°
∴弧DE的长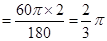
∴该圆锥的底面半径为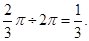
考点:本题考查的是勾股定理,圆锥的底面半径
点评:解答本题的关键是由BE=1,AE=2,判断出∠BAE=30°,同时熟记弧长公式: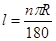 ,注意在使用公式时度不带单位.
,注意在使用公式时度不带单位.

练习册系列答案
相关题目

 如图,已知矩形纸片ABCD,AD=2,AB=
如图,已知矩形纸片ABCD,AD=2,AB=
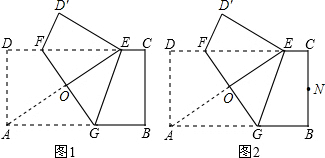 A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.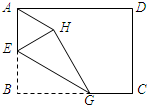 (2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )
(2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )