题目内容
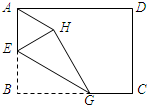 (2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )
(2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )分析:根据折叠的性质可得∠BEG=∠HEG,BE=EH,从而得出∠EAH=∠EHA,根据∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,可得∠BEG=∠EAH,继而可得出答案.
解答:解:由折叠的性质得,∠BEG=∠HEG,BE=EH,
故可得∠EAH=∠EHA(等腰三角形的性质),
∵∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,
∴∠BEG=∠HEG=∠EAH=∠EHA,
故与∠BEG相等的角的个数为3个.
故选B.
故可得∠EAH=∠EHA(等腰三角形的性质),
∵∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,
∴∠BEG=∠HEG=∠EAH=∠EHA,
故与∠BEG相等的角的个数为3个.
故选B.
点评:此题考查了折叠的性质,根据题意得出∠BEG=∠HEG,BE=EH,利用等腰三角形的性质解答是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
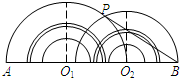 (2012•安庆二模)如图,大小两个量角器的零度线都在直线AB上,而且小量角器的中心在大量角器的外边缘上.如果它们外边缘上的公共点P在大量角器上对应的度数为50°,那么∠PBA为的度数( )
(2012•安庆二模)如图,大小两个量角器的零度线都在直线AB上,而且小量角器的中心在大量角器的外边缘上.如果它们外边缘上的公共点P在大量角器上对应的度数为50°,那么∠PBA为的度数( ) (2012•安庆二模)如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q、与y轴相交于点M(0,4)和N(0,16),则点P的坐标是
(2012•安庆二模)如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q、与y轴相交于点M(0,4)和N(0,16),则点P的坐标是