题目内容
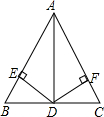
已知：如图，AD平分∠BAC，DE⊥AB，DF⊥AC，DB=DC，
求证：△ABC是等腰三角形．
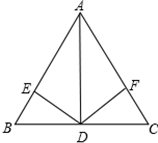
求证：△ABC是等腰三角形．
证明：∵AD平分∠BAC（已知），
∴AD是△ABC顶角的角平分线（角平分线的定义），
∵DE⊥AB，DF⊥AC（已知），
∴DE=DF（角平分线的性质），
在Rt△BDE和Rt△CDF中，
，
∴△BDE≌△CDF（HL）．
∴∠B=∠C（对应角相等），
∴△ABC是等腰三角形．
∴AD是△ABC顶角的角平分线（角平分线的定义），
∵DE⊥AB，DF⊥AC（已知），
∴DE=DF（角平分线的性质），
在Rt△BDE和Rt△CDF中，
|
∴△BDE≌△CDF（HL）．
∴∠B=∠C（对应角相等），
∴△ABC是等腰三角形．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
