��Ŀ����
����Ŀ���Ķ����в��ϣ������������⣺
���ɶ���a+b=c��������һ������a��b��c�ķ��̣�����֪�����������������⣬����÷��̵��������⣨a��b��c��ͨ�������������飮���ڹ���������о��ҹ���ʷ���зdz��Ի͵ijɾͣ������ҹ��Ŵ���ѧ�顶�����㾭�����أ���Լ��Ԫǰ1100�꣬���Ǿ��Ѿ�֪�����������������ġ������塱�����˰ѽ϶̵�ֱ�DZ߳�Ϊ�����ϳ���ֱ�DZ߳�Ϊ�ɣ���б����Ϊ�ң�����֪���˹������飨3��4��5�������Ƶأ������Եõ����й������飺��3��4��5������5��12��13������7��24��25������9��40��41�������ȵȣ���Щ����Ҳ�����ϴ����˹�������飮
������������Ĺ��ɣ��������������ֱ�۱�ʾ��
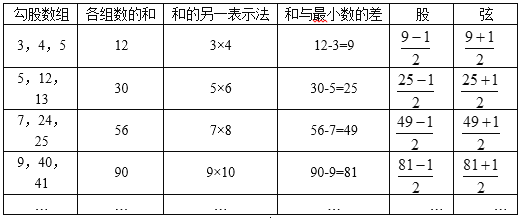
�۲���������������飬���Կ������Ǿ��������ص㣺
�ص�1����С�Ĺ�������ƽ�������������������ĺͣ�
�ص�2��____________________________________��
��
ѧϰ����
��1��������д���������������һ���ص㣺________________��
��2�����n��ʾ��1�������������������������Ա�ʾΪ��n��______��______��
��3������֤����2���Ľ��ۣ�
���𰸡���1����С�Ĺ������������1�������ij˻����ڸ����������ĺͣ���2��![]() ��
��![]() ����3����������
����3����������
��������
��1����3��4=3+4+5��5��6=5+12+13��7��8=7+24+25�������ɵ���С�Ĺ������������1�������ij˻����ڸ����������ĺͣ����ɵô𰸣�
��2����![]() ��
��![]() ��
��![]() ��
��![]() =13��
=13��![]() ��
��![]() �����ɵù���Ϊ����1������ʱ���������ڹ�����ƽ����1��һ�룬�������ڹ�����ƽ����1��һ�룬���ɵô𰸣�
�����ɵù���Ϊ����1������ʱ���������ڹ�����ƽ����1��һ�룬�������ڹ�����ƽ����1��һ�룬���ɵô𰸣�
��3��������ʽ������ó�n2+(![]() )2=(
)2=(![]() )2���ɣ�
)2���ɣ�
��1��3��4=3+4+5��
5��6=5+12+13��
7��8=7+24+25��
����
����С�Ĺ������������1�������ij˻����ڸ����������ĺͣ�
�ʴ�Ϊ����С�Ĺ������������1�������ij˻����ڸ����������ĺ�
��2��
![]() ��
��![]() ��
��
![]() ��
��![]() =13��
=13��
![]() ��
��![]() ��
��
����
��������ڹ�����ƽ����1��һ�룬�������ڹ�����ƽ����1��һ�룬
���Ϊ����1������ʱ���������ڹ�����ƽ����1��һ�룬�������ڹ�����ƽ����1��һ�룬
��nΪ��1�������ʱ����������������Ա�ʾΪ��n��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]()
��3����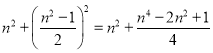
=![]()
=![]()
=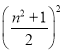 ��
��
�ࣨ![]() ��
��![]() ��
��![]() ���ǹ������飮
���ǹ������飮

 ��У����ϵ�д�
��У����ϵ�д�