Question

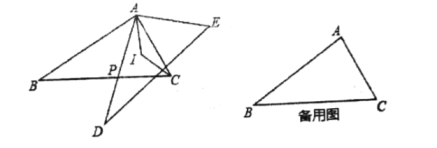
【题目】如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB。

（1）△BPQ是 三角形；

（2）求PQ的长度；

（3）求∠APB的度数。

Answer 1

【答案】（1）等边；（2）PQ=4；（3）∠APB=150°

【解析】

（1）连接PQ，由旋转的性质可得△BAP≌△BCQ，可推出BP=BQ，∠PBQ=60°，进而得到等边△BPQ；

（2）△BPQ为等边三角形，所以PQ=PB=4；

（3）由PQ=4，CQ=3，PC=5，可得出△PCQ为直角三角形，∠PQC=90°，由∠APB=∠CQB可得结果.

（1）连接PQ，

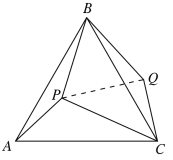
由旋转的性质可得△BAP≌△BCQ,

∴∠ABP=∠CBQ，BP=BQ，

又∵∠ABC=60°，

∴∠ABP+∠PBC=60°

∴∠CBQ+∠PBC=60°，即∠PBQ=60°，

∴△BPQ为等边三角形，

（2）∵△BPQ为等边三角形，

∴PQ=PB=4

（3）∵△BAP≌△BCQ，

∴CQ=PA=3，

在△PCQ中，PQ=4，CQ=3，PC=5，

∵32+42=52，即CQ2+PQ2=PC2，

∴△PCQ为直角三角形，∠PQC=90°，

又∵△BPQ为等边三角形，

∴∠BQP=60°，

∴∠CQB=∠BQP+∠PQC=150°

∵△BAP≌△BCQ,

∴∠APB=∠CQB=150°.