Question

（2013•黄石）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为（　　）

• A．

  9

  5

• B．

  21

  5

• C．

  18

  5

• D．

  5

  2

Answer 1

分析：先根据勾股定理求出AB的长，过C作CM⊥AB，交AB于点M，由垂径定理可知M为AD的中点，由三角形的面积可求出CM的长，在Rt△ACM中，根据勾股定理可求出AM的长，进而可得出结论．

解答：解：∵在Rt△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB=

AC2+BC2

=

33+42

=5，
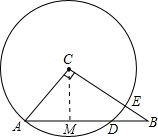过C作CM⊥AB，交AB于点M，如图所示，
∵CM⊥AB，
∴M为AD的中点，
∵S_△ABC=

1

2

AC•BC=

1

2

AB•CM，且AC=3，BC=4，AB=5，
∴CM=

12

5

，
在Rt△ACM中，根据勾股定理得：AC²=AM²+CM²，即9=AM²+（

12

5

）²，
解得：AM=

9

5

，
∴AD=2AM=

18

5

．
故选C．

点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．