题目内容
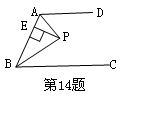
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它
们的面积分别为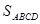 和
和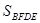 ,现给出下列命题:
,现给出下列命题:
①若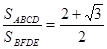 ,则
,则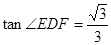 ; ②若
; ②若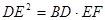 ,则DF=2AD
,则DF=2AD
则
们的面积分别为
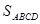 和
和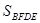 ,现给出下列命题:
,现给出下列命题:①若
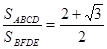 ,则
,则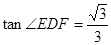 ; ②若
; ②若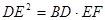 ,则DF=2AD
,则DF=2AD则
| A.①是真命题,②是真命题 | B.①是真命题,②是假命题 |
| C.①是假命题,②是真命题 | D.①是假命题,②是假命题 |
A
分析:①由已知先求出sin∠EDF,再求出tan∠EDF,确定是否真假命题.②由已知根据矩形、菱形的性质用面积法得出结论.
解答: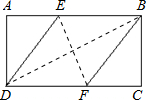 解:①设CF=x,DF=y,BC=h,则由已知菱形BFDE,BF=DF=y
解:①设CF=x,DF=y,BC=h,则由已知菱形BFDE,BF=DF=y
由已知得: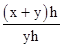 =
=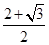 ,
,
得: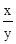 =
=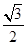 ,即cos∠BFC=
,即cos∠BFC=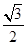 ,
,
∴∠BFC=30°,
由已知
∴∠EDF=30°
∴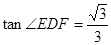 ,
,
所以①是真命题.
②已知菱形BFDE,∴DF=DE
S△DEF=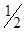 DF?AD=
DF?AD=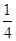 BD?EF,
BD?EF,
又DE2=BD?EF(已知),
∴S△DEF=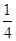 DE2=
DE2=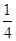 DF2,
DF2,
∴DF?AD=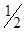 DF2,
DF2,
∴DF=2AD,
所以②是真命题.
故选:A.
解答:
 解:①设CF=x,DF=y,BC=h,则由已知菱形BFDE,BF=DF=y
解:①设CF=x,DF=y,BC=h,则由已知菱形BFDE,BF=DF=y由已知得:
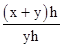 =
=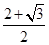 ,
, 得:
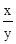 =
=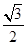 ,即cos∠BFC=
,即cos∠BFC=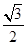 ,
,∴∠BFC=30°,
由已知
∴∠EDF=30°
∴
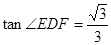 ,
,所以①是真命题.
②已知菱形BFDE,∴DF=DE
S△DEF=
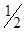 DF?AD=
DF?AD=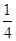 BD?EF,
BD?EF,又DE2=BD?EF(已知),
∴S△DEF=
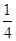 DE2=
DE2=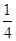 DF2,
DF2,∴DF?AD=
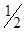 DF2,
DF2,∴DF=2AD,
所以②是真命题.
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目