题目内容
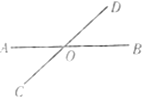
【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=30°,求∠A的度数;
(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.

【答案】(1)∠A=60°;(2)存在,∠DFB=∠DBF.
【解析】
(1)根据角平分线的定义得到∠EBC=2∠DBC=60°,∠ABC=2∠EBC=120°,根据平行线的性质得到∠A+∠ABC=180°,于是得到结论;
(2)设∠DBC=x°,则∠ABC=2∠ABE=(4x)°,根据已知条件得到∠ABF=(![]() x-90)°,求得∠DBF=(90-
x-90)°,求得∠DBF=(90-![]() x)°,根据平行线的性质得到∠DFB+∠CBF=180°,于是得到∠DFB=(90-
x)°,根据平行线的性质得到∠DFB+∠CBF=180°,于是得到∠DFB=(90-![]() x)°,即可得到结论.
x)°,即可得到结论.
解:(1)∵BD平分∠EBC,∠DBC=30°,
∴∠EBC=2∠DBC=60°.
∵BE平分∠ABC,
∴∠ABC=2∠EBC=120°.
∵AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=60°.
(2)存在∠DFB=∠DBF.理由如下:
设∠DBC=x°,则∠ABC=2∠ABE=(4x)°.
∵7∠DBC-2∠ABF=180°,
∴(7x)°-2∠ABF=180°,
∴∠ABF=(![]() x-90)°,
x-90)°,
∴∠CBF=∠ABC-∠ABF=(![]() x+90)°,
x+90)°,
∠DBF=∠ABC-∠ABF-∠DBC=(90-![]() x)°.
x)°.
∵AD∥BC,
∴∠DFB+∠CBF=180°,
∴∠DFB=(90-![]() x)°,
x)°,
∴∠DFB=∠DBF.

练习册系列答案
相关题目