题目内容
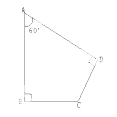
【题目】如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)求证:AD+BE=DE;
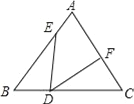
(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.

【答案】(1)见解析;(2)见解析;(3)DE+BE=AD,理由见解析
【解析】试题分析:(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
(2)由(1)得到AD=CE,CD=BE,即可求出答案;
(3)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,代入已知即可得到答案.
试题解析:
(1)如图1,∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
∵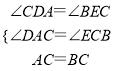 ,
,
∴△ADC≌△CEB;
∴DC=BE,AD=EC,
∵DE=DC+EC,
∴DE=BE+AD.
(2)解:DE+BE=AD.理由如下:
如图2,∵∠ACB=90°,
∴∠ACD+∠BCE=90°.
又∵AD⊥MN于点D,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,
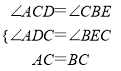 ,
,
∴△ACD≌△CBE(AAS),
∴CD=BE,AD=CE,
∴DE+BE=DE+CD=EC=AD,即DE+BE=AD.

练习册系列答案
相关题目