题目内容
【题目】如图,点E、F为菱形ABCD对角线BD的三等分点.
(1)试判断四边形AECF的形状,并加以证明;
(2)若菱形ABCD的周长为52,BD为24,试求四边形AECF的面积.
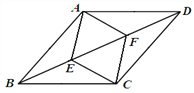
【答案】(1)菱形;(2) 40
【解析】试题分析:(1)根据菱形的对角线互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,然后根据对角线互相垂直平分的四边形是菱形证明;
(2)根据菱形的四条边都相等求出边长AB,根据菱形的对角线互相平分求出OB,然后利用勾股定理列式求出AO,再求出AC,最后根据菱形的面积等于对角线乘积的一半列式计算即可得解.
试题解析:
(1)四边形ABCD为菱形.
理由如下:如图,连接AC交BD于点O,
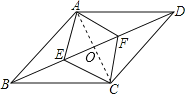
∵四边形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,
∴BE=FD,
∴BO=OD,
∵AO=OC,
∴四边形ABCD为平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形;
(2)∵四边形ABCD为菱形,且周长为52,
∴AB=13,
∵BD=24,E、F为菱形ABCD对角线BD的三等分点,
∴OB=![]() BD=
BD=![]() ×24=12,EF=
×24=12,EF=![]() ,
,
由勾股定理得,AO=![]() ,
,
∴AC=2AO=2×5=10,
∴S四边形AECF=![]() EFAC=
EFAC=![]() ×8×10=40.
×8×10=40.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目