题目内容
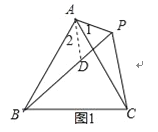
【题目】如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.

(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
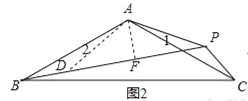
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.
【答案】(1)BP=4;(2)PA+PC=PB;(3)![]() PA+PC=PB.
PA+PC=PB.
【解析】
试题分析:(1)AB=AC,∠BAC=60°,证得△ABC是等边三角形,∠APB=∠ABC,得到∠APB=60°,又点P恰巧在∠ABC的平分线上,得到∠ABP=30°,得到直角三角形,利用直角三角形的性质解出结果.
(2)在BP上截取PD,使PD=PA,连结AD,得到△ADP是等边三角形,再通过三角形全等证得结论.
(3)以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,得到等腰三角形,然后通过三角形全等证得结论.
试题解析:解:(1)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∠APB=∠ABC,
∴∠APB=60°,
又∵点P恰巧在∠ABC的平分线上,
∴∠ABP=30°,
∴∠PAB=90°,
∴BP=2AP,
∵AP=2,
∴BP=4;
(2)结论:PA+PC=PB.
证明:如图1,在BP上截取PD,使PD=PA,连结AD,
∵∠APB=60°,
∴△ADP是等边三角形,
∴∠DAP=60°,
∴∠1=∠2,PA=PD,
又AB=AC,
∴△ABD≌△ACP,
∴PC=BD,
∴PA+PC=PB;
(3)结论:![]() PA+PC=PB.
PA+PC=PB.
证明:如图2,以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,
∴AP=AD,
∵∠BAC=120°,
∴∠ABC=30°,
∴∠APB=30°,
∴∠DAP=120°,
∴∠1=∠2,
又AB=AC,
∴△ABD≌△ACP,
∴BD=PC,
∵AF⊥PD,
∴PF=![]() AP,
AP,
∴PD=![]() AP,
AP,
∴![]() PA+PC=PB.
PA+PC=PB.

 阅读快车系列答案
阅读快车系列答案