题目内容
4、如图，圆内接四边形ABCD中，AC、BD交于E点，且BC=DC，则图中共有相似三角形（ ）
分析：根据圆周角定理，得∠BAC=∠CAD=∠BDC，∠CBD=∠CAD，∠ABD=∠ACD，∠ACB=∠ADB，再根据两角对应相等即可找到所有的相似三角形．
解答：解：根据圆周角定理，得∠BAC=∠CAD=∠BDC，∠CBD=∠CAD，∠ABD=∠ACD，∠ACB=∠ADB，
∴△ABE∽△DCE∽△ACD，△BCE∽△ADE∽△ABC．
共6对．
故选C．
∴△ABE∽△DCE∽△ACD，△BCE∽△ADE∽△ABC．
共6对．
故选C．
点评：此题综合考查了圆周角定理的推论和相似三角形的判定．
练习册系列答案
相关题目
11、如图，圆内接四边形ABCD的对角线AC，BD把四边形的四个内角分成八个角，这八个角中相等的角的对数至少有（ ）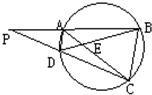
15、如图，圆内接四边形ABCD的BA，CD的延长线交于P，AC，BD交于E，则图中相似三角形有（ ）
2、已知：如图，圆内接四边形ABCD中，∠BAD=65°，则∠BCD=
已知：如图，圆内接四边形ABCD，过C点作对角线BD的平行线交AD的延长线于E点．
如图，圆内接四边形ABCD，AB=AD，∠BAD=60°，AC=2，则四边形ABCD的面积为（ ）| A、4 | ||
| B、2 | ||
C、
| ||
D、
|