题目内容
如图,AB是⊙O的直径,弦CE⊥AB交AB于点D,点P在AB的延长线上, 连结OE、AC、BC,已知∠POE=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)若BD=2OD,且PB=12,求⊙O的半径.

(1)求证:PC是⊙O的切线;
(2)若BD=2OD,且PB=12,求⊙O的半径.
通过角度的变换求证;6
试题分析:.(1)证明:连结OC,因为CE⊥AB,OC="OE,"
所以
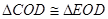 ,所以
,所以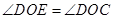 , 2分
, 2分又因为
 ,所以
,所以 3分
3分又因为
 ,所以
,所以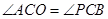 , 4分
, 4分而AB是⊙O的直径,所以
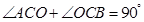 , .5分
, .5分所以
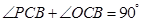 ,即OC⊥CP,所以PC是⊙O的切线. 6分
,即OC⊥CP,所以PC是⊙O的切线. 6分(2)解:因为
 ,所以
,所以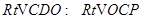 , 7分
, 7分所以
 ,
,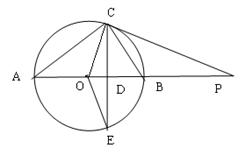
又因为BD=2OD,所以OC=3OD,
又PB=12,所以
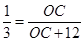 ,
,解得OC=6,即⊙O的半径等于6.
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 垂直于射线AM,垂足为点D.
垂直于射线AM,垂足为点D.
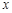 °,∠ECD=
°,∠ECD=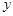 °,⊙B的半径为R,则
°,⊙B的半径为R,则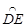 的长度是( )
的长度是( )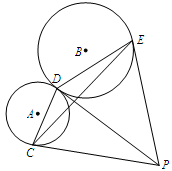




 是Rt
是Rt ABC的外接圆,
ABC的外接圆,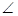 ABC=90
ABC=90 ,点P是
,点P是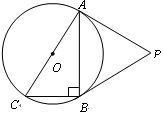
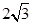 ,BC=2,求
,BC=2,求
 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出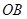 上,当
上,当 ∽
∽ 的长度.
的长度. 

