题目内容
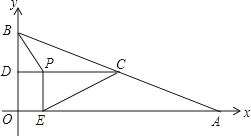
【题目】如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠DAB+∠ABC=180° B. AB=BC
C. AB=CD,AD=BC D. ∠ABC=∠ADC,∠BAD=∠BCD
【答案】A
【解析】
首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,则四边形ABCD为菱形.所以根据菱形的性质进行判断.
四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形)
∴AB=CD,AD=BC,∠ABC=∠ADC,∠BAD=∠BCD,故C、D正确;
过点D分别作AB,BC边上的高为AE,AF.则
AE=AF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD中,S四边形ABCD=S四边形ABCD,即AB×AF=BC×AE,
∴AB=BC.故B正确;
∴平行四边形ABCD为菱形(邻边相等的平行四边形是菱形).
只有在四边形ABCD是矩形时,∠DAB+∠DCB=180°,故A不正确.
故选:A

 阅读快车系列答案
阅读快车系列答案【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.