题目内容
二次函数y=x2+bx+c的图象如图所示，则其对称轴是________，当函数值y＜0时，对应x的取值范围是________．
x=-1 -3＜x＜1
分析：根据抛物线与x轴的两交点到对称轴的距离相等，得对称轴为x=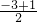
=-1；
函数值y＜0时，即函数图象位于x轴的下方，此时x的取值范围是-3＜x＜1．
解答：∵物线与x轴的两交点到对称轴的距离相等，
∴对称轴为x=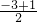=-1，
∵函数值y＜0时，即函数图象位于x轴的下方，
根据图象可知当-3＜x＜1时，函数图象位于x轴的下方，
∴当-3＜x＜1时，函数值y＜0．
故答案为x=-1；-3＜x＜1．
点评：本题考查了二次函数图象的性质及根据二次函数的图象求相应的二次不等式的知识，是近几年中考的重要考点之一．
分析：根据抛物线与x轴的两交点到对称轴的距离相等，得对称轴为x=
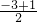=-1；函数值y＜0时，即函数图象位于x轴的下方，此时x的取值范围是-3＜x＜1．
解答：∵物线与x轴的两交点到对称轴的距离相等，
∴对称轴为x=
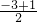=-1，∵函数值y＜0时，即函数图象位于x轴的下方，
根据图象可知当-3＜x＜1时，函数图象位于x轴的下方，
∴当-3＜x＜1时，函数值y＜0．
故答案为x=-1；-3＜x＜1．
点评：本题考查了二次函数图象的性质及根据二次函数的图象求相应的二次不等式的知识，是近几年中考的重要考点之一．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目