题目内容
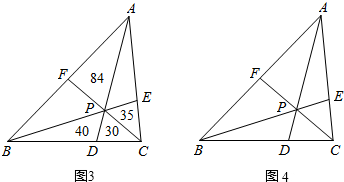
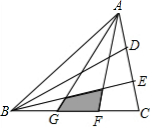
如图,设O为△ABC内一点,连接AO、BO、CO,并延长交BC、CA、AB于点D、E、F,已知S△AOB:S△BOC:S△AOC=3:4:6.则
•
•
等于( )

| OD |
| AO |
| OE |
| BO |
| OF |
| CO |
A.
| B.
| C.
| D.
|

∵S△AOB:S△BOC:S△AOC=3:4:6,
∴S△AOB:S△ABC=3:13,S△BOC:S△ABC=4:13,S△AOC:S△ABC=6:13,
∴
=
,
=
,
=
,
∴
=
,
=
,
=
,
∴
•
•
=
×
×
=
.
故选:B.
∴S△AOB:S△ABC=3:13,S△BOC:S△ABC=4:13,S△AOC:S△ABC=6:13,
∴
| OF |
| CF |
| 3 |
| 13 |
| OD |
| AD |
| 4 |
| 13 |
| OE |
| BE |
| 6 |
| 13 |
∴
| OF |
| CO |
| 3 |
| 10 |
| OD |
| AO |
| 4 |
| 9 |
| OE |
| BO |
| 6 |
| 7 |
∴
| OD |
| AO |
| OE |
| BO |
| OF |
| CO |
| 3 |
| 10 |
| 4 |
| 9 |
| 6 |
| 7 |
| 4 |
| 35 |
故选:B.

练习册系列答案
相关题目