题目内容
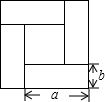 如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式
如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式(a+b)2-(a-b)2=4ab
(a+b)2-(a-b)2=4ab
.分析:用大正方形的面积减去小正方形的面积表示四个矩形纸片的面积,也可以直接利用矩形的面积公式表示,两种方法表示的面积相等列式即可得解.
解答:解:四个矩形的面积为:(a+b)2-(a-b)2,
也可以表示为4ab,
所以,恒等式为:(a+b)2-(a-b)2=4ab.
故答案为:(a+b)2-(a-b)2=4ab.
也可以表示为4ab,
所以,恒等式为:(a+b)2-(a-b)2=4ab.
故答案为:(a+b)2-(a-b)2=4ab.
点评:本题考查了完全平方公式的几何背景,仔细观察图形,用两种方法表示出四个矩形的面积是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
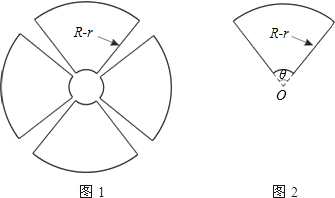 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;

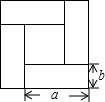 如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式________.
如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式________.