题目内容
一园林设计师要使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成,为使得绿化效果最佳,还须使得扇环面积最大.(1)求使图1花圃面积为最大时R-r的值及此时花圃面积,
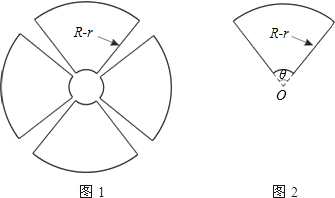 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;(2)若L=160m,r=10m,求使图2面积为最大时的θ值.
分析:(1)要求图1花圃面积,就要求出一个大扇形减一个小扇形的面积,然后再利用函数分析讨论最大值.
设图2扇环的圆心角为θ,面积为S,根据题意得:L=
+
+2(R-r)=θ•
+2(R-r).求出θ,S的关系式.最后可求得S在R-r=
时为最大,最大值为
.
(2)把值代入上式计算即可.根据(1)可得当R-r=
时,S取值最大.把L的值代入可得解.
设图2扇环的圆心角为θ,面积为S,根据题意得:L=
| θπR |
| 180 |
| θπr |
| 180 |
| π(R+r) |
| 180 |
| L |
| 4 |
| L2 |
| 16 |
(2)把值代入上式计算即可.根据(1)可得当R-r=
| L |
| 4 |
解答:解:(1)若使形如图1花圃面积为最大,则必定要求图2扇环面积最大.
设图2扇环的圆心角为θ,面积为S,根据题意得:L=
+
+2(R-r),(2分)
L=θ•
+2(R-r)
180L-360(R-r)=π(R+r)θ
∴θ=
.(3分)
∴S=
-
=
•θ•(R2-r2)(4分)
=
•
•(R2-r2)
=
[L-2(R-r)]•(R-r)=-[(R-r)-
]2+
.(5分)
∵式中0<R-r<
,
∴S在R-r=
时为最大,最大值为
.(6分)
∴花圃面积最大时R-r的值为
,最大面积为
×4=
.(7分).
(2)∵当R-r=
时,S取值最大,
∴R-r=
=
=40(m),R=40+r=40+10=50(m).(8分)
∴θ=
=
=
(度).(10分)
设图2扇环的圆心角为θ,面积为S,根据题意得:L=
| θπR |
| 180 |
| θπr |
| 180 |
L=θ•
| π(R+r) |
| 180 |
180L-360(R-r)=π(R+r)θ
∴θ=
| 180[L-2(R-r)] |
| π(R+r) |
∴S=
| θπR2 |
| 360 |
| θπr2 |
| 360 |
| π |
| 360 |
=
| π |
| 360 |
| 180[L-2(R-r)] |
| π(R+r) |
=
| 1 |
| 2 |
| L |
| 4 |
| L2 |
| 16 |
∵式中0<R-r<
| L |
| 2 |
∴S在R-r=
| L |
| 4 |
| L2 |
| 16 |
∴花圃面积最大时R-r的值为
| L |
| 4 |
| L2 |
| 16 |
| L2 |
| 4 |
(2)∵当R-r=
| L |
| 4 |
∴R-r=
| L |
| 4 |
| 160 |
| 4 |
∴θ=
| 180[L-2(R-r)] |
| π(R+r) |
| 180×(160-2×40) |
| π×60 |
| 240 |
| π |
点评:本题综合考查了扇形的面积计算和函数有关知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


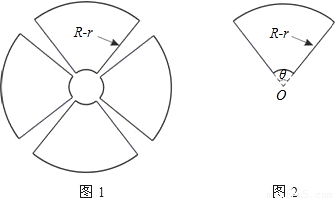 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;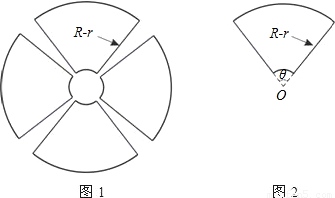 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;