题目内容
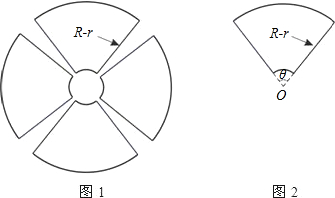
一园林设计师要使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成,为使得绿化效果最佳,还须使得扇环面积最大.

(1)求使图1花圃面积为最大时R-r的值及此时花圃面积,其中R、r分别为大圆和小圆的半径;
(2)若L=160m,r=10m,求使图2面积为最大时的θ值.
【答案】
(1)花圃面积最大时 的值为
的值为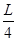 ,最大面积为
,最大面积为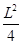 (2)
(2)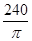 度
度
【解析】解:(1)若使形如图1花圃面积为最大,则必定要求图2扇环面积最大.
设图2扇环的圆心角为θ,面积为S,根据题意得:
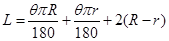 ,
………………………2分
,
………………………2分
= .
.
∴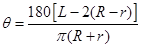 .
……………………………3分
.
……………………………3分
∴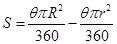 =
=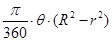 ……………………………4分
……………………………4分
=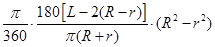
=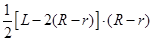 =
=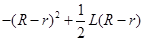
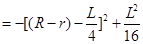
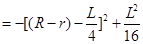 .
……………………………5分
.
……………………………5分
∵式中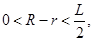 ∴S在
∴S在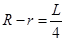 时为最大,最大值为
时为最大,最大值为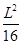 . ………6分
. ………6分
∴花圃面积最大时 的值为
的值为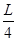 ,最大面积为
,最大面积为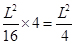 . ……………7分
. ……………7分
(2)∵当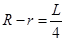 时,S取值最大,
时,S取值最大,
∴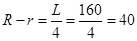 (m),
(m),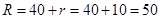 (m). …………………………8分
(m). …………………………8分
∴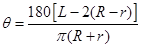 =
=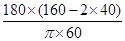 =
=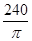 (度). ………………………10分
(度). ………………………10分
(1)由于花圃是由四个形状、大小完全一样的扇环面组成,则图1 一个扇环的周长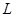 等于两个扇形的弧长与两个
等于两个扇形的弧长与两个 的和,根据弧长公式得到
的和,根据弧长公式得到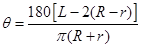 ,再根据扇形面积公式,化简得
,再根据扇形面积公式,化简得
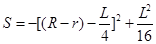 ,根据二次函数的最值即可解决问题
,根据二次函数的最值即可解决问题
(2)根据(1)中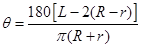 ,可以求出
,可以求出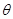 值
值

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;
 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;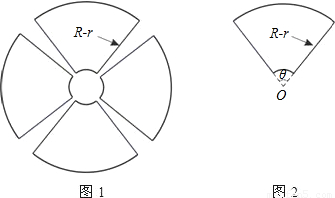 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;