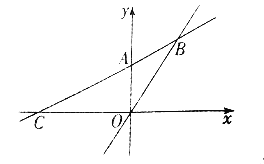
��Ŀ����
����Ŀ����ͼ����֪l1��l2����O��l1��l2�����У���O�İ뾶Ϊ2cm������ABCD�ı�AD��AB�ֱ���l1��l2�غϣ�AB��![]() cm��AD��4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt(s)��
cm��AD��4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt(s)��
(1)��ͼ�٣�����OA��AC�����OAC�Ķ���Ϊ �㣻
(2)��ͼ�ڣ�����ͼ���ƶ�һ��ʱ���O�����O1��λ�ã�����ABCD����A1B1C1D1��λ�ã���ʱ��O1��A1��C1ǡ����ͬһֱ���ϣ���Բ��O�ƶ��ľ���(��OO1�ij�����
(3)���ƶ������У�Բ��O�����ζԽ���AC����ֱ�ߵľ����ڲ��ϱ仯����þ���Ϊd(cm)����d<2ʱ����t��ȡֵ��Χ�������ʱ�������ñ���ͼ�������ʾ��ͼ��

���𰸡���1��105����2��![]() ����3��
����3��![]() ��t��
��t��![]() .
.
�������������������1����O��l1��l2�����У�����Բ�ĺ������е㣬��������.OA��Ϊ�����εĶԽ��ߣ��õ���OAD=450������Rt��ADC�У���������Ǻ�������DAC=600���Ӷ������OAC�Ķ���1050.
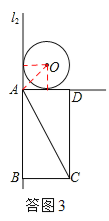
��2������O1���е�E����O1E=2��O1E��l1��������O1EA1�ס�D1C1E1,��A1E=![]() ������2+O1O+A1E=AA1������t���������Բ���ƶ��ľ���3t=
������2+O1O+A1E=AA1������t���������Բ���ƶ��ľ���3t=![]() .
.
��3��Բ��O���Խ���AC�ľ���d��2����d��r.˵����O��AC�ཻ�����Գ��������ٽ���tֵ������O��AC���У��˶��д����������е�λ��.�ֱ�����������ʱt��ֵ�����ɵó�d��rʱ��t��ȡֵ
����������⣺��1��1050.
��2��O1��A1��C1ǡ����ͬһֱ����ʱ������O��AC���е�ΪE������O1E�����ͼ1��
�ɵ�O1E=2��O1E��l1��
��Rt��A1D1C1����A1D1=4��D1C1=![]() ��
��
��tan��C1A1D1=![]() �����C1A1D1=600��
�����C1A1D1=600��
��Rt��A1O1E��, ��O1A1E=��C1A1D1=600����A1E=![]() ,
,
��![]() ����
����![]() ����
����![]() .
.
��OO1=3t=![]() .
.
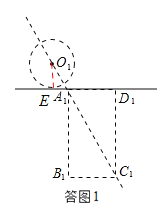
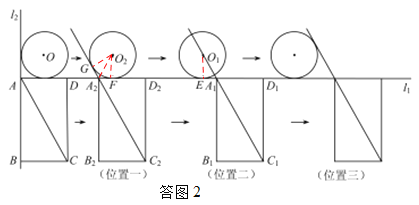
��3�����ͼ2��
����ֱ��AC����O��һ������ʱ�����ƶ�ʱ��Ϊt1.��λ��һ����ʱ��O�ƶ�����O2��λ�ã�����ABCD�ƶ���A2B2C2D2��λ��.
����O2��ֱ��l1��A2C2�ֱ������ڵ�F��G, ����O2F��O2G��O2A2��
��O2F��l1��O2G��A2C2.
���ɣ�2���ɵ���C2A2D2=600�ڣ����GA2F=1200�����O2A2F=600.
��Rt��O2A2F��O2F=2����A2F=![]() .
.
��OO2=3t1�� ![]() ����
����![]() �����
�����![]() .
.
������O1��A1��C1ǡ����ͬһֱ����ʱΪλ�ö������ƶ�ʱ��Ϊt2.�ɣ�2���ɵ�![]() .
.
����ֱ��AC����O�ڶ�������ʱ�����ƶ�ʱ��Ϊt3����λ��3��������֪����λ��һ��λ�ö�����ʱ����λ�ö���λ��������ʱ�����.
��![]() ����
����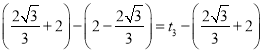 �����
�����![]() .
.
������������d<2ʱ��t��ȡֵ��ΧΪ![]() ��t��
��t��![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�