题目内容
【题目】如图，在平面直角坐标系中，一次函数的图象经过点
，且与正比例函数
的图象相交于点
，与x轴相交于点
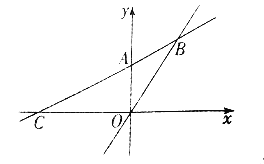
（1）求m的值及一次函数的表达式.
（2）求△BOC的面积.
【答案】（1）
， 
；（2）6
【解析】试题分析：（1）将点B(2,m)代入正比例函数
中即可得出m的值，设一次函数的解析式为yAB=kx+b，再用待定系数法求函数解析式；
（2）由一次函数求得点C的坐标，得出OC的长度，根据S△BOC＝
计算得出.
试题解析：
(1)∵点B(2,m)在正比例函数
的图象上，
∴m=3,
∴点B的坐标是(2,3);
设一次函数解析式为yAB=kx+b，且点A（0，2）、B（2，3）在函数的图象上
∴
解得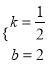
∴一次函数的解析式：yAB=
x+2.
(2)∵ 直线yAB=
x+2与x轴交点坐标为(-4,0),
∴OC=4,
∴S△BOC＝
=
=6.
练习册系列答案
相关题目
【题目】上周“双十二”瑞安某书店开展优惠购书活动：各类课外书活动时每本销售价格为y元，活动前每本销售价格为x（
）元，且y是x的一次函数，其中A类课外书与B类课外书活动前与活动时的价格如下表：
图书类别 | 活动前的每本销售价格x（单位：元） | 活动时的每本销售价格y （单位：元） |
A类 | 28 | 21 |
B类 | 21 | 18 |
（1）求y关于x的一次函数表达式.
（2）当天小明购买了一本课外书，花费了24元，该课外书活动前的每本销售价格是多少元？
（3）在“双十二”优惠活动中，某学校花费不超过1900元，购买A、B两类课外书共100本，且B类课外书不超过70本，则可能有哪几种购书方案？
