Question

如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=

5

．下列结论：①△APD≌△AEB；②点B到直线AE的距离为

2

；③EB⊥ED；④S_△APD+S_△APB=1+

6

；⑤S_{正方形ABCD}=4+

6

．其中正确结论的序号是______．

Answer 1

由边角边定理易知△APD≌△AEB，故①正确；
由△APD≌△AEB得，∠AEP=∠APE=45°，从而∠APD=∠AEB=135°，
所以∠BEP=90°，
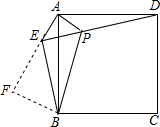
过B作BF⊥AE，交AE的延长线于F，则BF的长是点B到直线AE的距离，
在△AEP中，由勾股定理得PE=

2

，
在△BEP中，PB=

5

，PE=

2

，由勾股定理得：BE=

3

，
∵∠PAE=∠PEB=∠EFB=90°，AE=AP，
∴∠AEP=45°，
∴∠BEF=180°-45°-90°=45°，
∴∠EBF=45°，
∴EF=BF，
在△EFB中，由勾股定理得：EF=BF=

6

2

，
故②是错误的；
因为△APD≌△AEB，所以∠ADP=∠ABE，而对顶角相等，所以③是正确的；
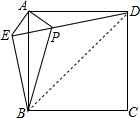
由△APD≌△AEB，
∴PD=BE=

3

，
可知S_△APD+S_△APB=S_△AEB+S_△APB=S_△AEP+S_△BEP=

1

2

+

6

2

，因此④是错误的；
连接BD，则S_△BPD=

1

2

PD×BE=

3

2

，
所以S_△ABD=S_△APD+S_△APB+S_△BPD=2+

6

2

，
所以S_{正方形ABCD}=2S_△ABD=4+

6

．
综上可知，正确的有①③⑤．