题目内容
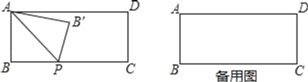
【题目】已知:矩形ABCD,AB=2,BC=5,动点P从点B开始向点C运动,动点P速度为每秒1个单位,以AP为对称轴,把△ABP折叠,所得△AB'P与矩形ABCD重叠部分面积为y,运动时间为t秒.
(1)当运动到第几秒时点B'恰好落在AD上;
(2)求y关于t的关系式,以及t的取值范围;
(3)在第几秒时重叠部分面积是矩形ABCD面积的![]() ;
;
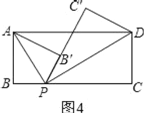
(4)连接PD,以PD为对称轴,将△PCD作轴对称变换,得到△PC'D,当t为何值时,点P、B'、C'在同一直线上?
【答案】(1)当运动到第2秒时点B′恰好落在AD上;(2)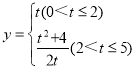 ;(3)第4秒时,重叠部分面积都是矩形ABCD面积的
;(3)第4秒时,重叠部分面积都是矩形ABCD面积的![]() ;(4)当t为1秒或4秒时,点P,B′,C′在同一直线上.
;(4)当t为1秒或4秒时,点P,B′,C′在同一直线上.
【解析】
(1)点B′落在AD上时,四边形ABPB′为正方形,所以t=2;
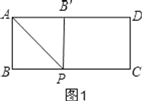
(2)分两种情况讨论:①当0≤t≤2时,如图2,重叠部分面积就是△APB′的面积,即△APB的面积;
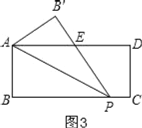
②当2<t≤5时,如图3,重叠部分面积就是△APE的面积,先根据勾股定理表示出AE的长,再利用面积公式求△APE的面积;
(3)分别将①和②中的y等于矩形ABCD面积的![]() ,求出对应的t值即可;
,求出对应的t值即可;
(4)点P,B′,C′在同一直线上时,△AB′P∽△PC′D,得![]() ,列一元二次方程,求出t的值即可.
,列一元二次方程,求出t的值即可.
解:(1)如图1,由折叠得:∠AB′P=∠B=90![]() ,AB=AB′=2,
,AB=AB′=2,
∵四边形ABCD为矩形,
∴∠BAB′=90![]() ,
,
∴四边形ABPB′为正方形,
∴BP=AB=2,
∵动点P速度为每秒1个单位,
∴t=2,
即当运动到第2秒时点B′恰好落在AD上;
(2)分两种情况:①当0≤t≤2时,如图2,PB=t,
由折叠得:S△AB′P=S△ABP,
∴y=S△ABP=![]() ABPB=
ABPB=![]() ×2×t=t,
×2×t=t,
②当2<t≤5时,如图3,
由折叠得:∠APB=∠APE,PB=PB′=t,
∵AD∥BC,
∴∠DAP=∠APB,
∴∠DAP=∠APE,
∴AE=PE,
设AE=x,则PE=x,B′E=t﹣x,
由勾股定理得:22+(t﹣x)2=x2,
x=![]() ,
,
∴![]() ,
,
综上所述: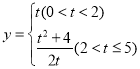 ;
;
(3)①y=t=![]() ×2×5,
×2×5,
∴t=2.5
②![]() =
=![]() ×2×5,
×2×5,
∴t1=1(舍),t2=4,
综上所述:在第4秒时,重叠部分面积都是矩形ABCD面积的![]() ;
;
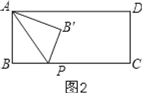
(4)如图4,点P,B′,C′在同一直线上,
由折叠得:∠APB=∠APB′,∠C′PD=∠CPD,
∴∠APC′+∠C′PD=![]() ×180°=90°,
×180°=90°,
∵∠PAB′+∠APB′=90°,
∴∠PAB′=∠C′PD,
∵∠AB′P=∠C′=90°,
∴△AB′P∽△PC′D,
∴![]() ,
,
∴![]() ,
,
解得:t1=1,t2=4,如图5所示,
∴当t为1秒或4秒时,点P,B′,C′在同一直线上.


 阅读快车系列答案
阅读快车系列答案【题目】商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了![]() 元.
元.
(1)填表:
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到最大时,则每台冰箱的实际售价应定为多少元?