Question

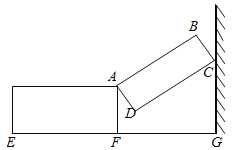
【题目】如图，一种侧面形状为矩形的行李箱，箱盖打开后，盖子的一端靠在墙上，此时BC=10cm，箱底端点E与墙角G的距离为65cm，∠DCG=60°．

（1）箱盖绕点A转过的角度为______，点B到墙面的距离为______cm；

（2）求箱子的宽EF（结果保留整数，可用科学计算器）．（参考数据：=1.41，=1.73）

Answer 1

【答案】（1）150°；5（2）32.4cm

【解析】

（1）如图，过点B作BH⊥CG于H，过点D作CG的垂线MN交AF于M，交HG于N．利用矩形的性质、直角三角形的性质以及等角的余角相等得到∠MAD=30°，根据周角的定义易求箱盖绕点A转过的角度；通过解直角△BHC来求BH的长度；

（2）通过解直角△AMD得到线段MD的长度，则DN=65-EF-DM，利用解直角△DCN来求CD的长度，即EF的长度即可．

（1）如图，过点B作BH⊥CG于H，过点D作CG的垂线MN交AF于M，交HG于N．

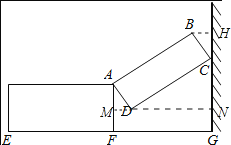
∵∠DCG=60°，

∴∠CDN=30°．

又∵四边形ABCD是矩形，

∴∠ADC=∠BCD=90°，

∴∠MAD=∠CDN=30°（同角的余角相等），

∴箱盖绕点A转过的角度为：360°-90°-30°-90°=150°．

在直角△BCH中，∠BCH=30°，BC=10cm，则BH=BC=5cm．

故答案是：150°；5；

（2）在直角△AMD中，AD=BC=10cm，∠MAD=30°，则MD=ADsin30°=×10=5（cm）．

∵∠CDN=30°，

∴cos∠CDN=cos30°=，即

解得EF=32.4．

即箱子的宽EF是32.4cm．