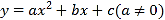题目内容
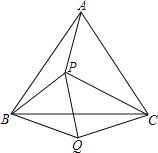
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)6;(2)![]() 的值为
的值为![]() 或
或![]() ;(3)当
;(3)当![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)根据勾股定理可以得到AC;
(2)过![]() 作
作![]() 于
于![]() ,求出AD=2,设
,求出AD=2,设![]() ,则
,则![]() ,根据勾股定理求出CP,根据P所走的路径为AB,BC,CP之和,求出t即可,注意P,D重合时也符合题意P所走的路径为AB,求出t即可.
,根据勾股定理求出CP,根据P所走的路径为AB,BC,CP之和,求出t即可,注意P,D重合时也符合题意P所走的路径为AB,求出t即可.
(3)①当![]() 在
在![]() 上且
上且![]() 时,根据
时,根据![]() ,而
,而![]() ,
,![]() ,求出CP=BP ,P为AB中点,即可求出;
,求出CP=BP ,P为AB中点,即可求出;
②当![]() 在
在![]() 上且
上且![]() 时,直接求出即可;
时,直接求出即可;
③当![]() 在
在![]() 上且
上且![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,根据△ADC∽△ACB,求出AD,即可求出AB,即可求出;
,根据△ADC∽△ACB,求出AD,即可求出AB,即可求出;
④当![]() 在
在![]() 上且
上且![]() 时,
时,![]() ,即可求出.
,即可求出.
解:(1)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ;
;
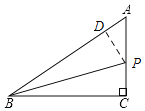
(2)如图,过![]() 作
作![]() 于
于![]() ,
,
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
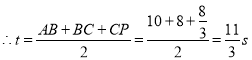 ;
;
当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 也在
也在![]() 的角平分线上,
的角平分线上,
此时,![]() ;
;
综上所述,点![]() 恰好在
恰好在![]() 的角平分线上,
的角平分线上,![]() 的值为
的值为![]() 或
或![]() ;
;
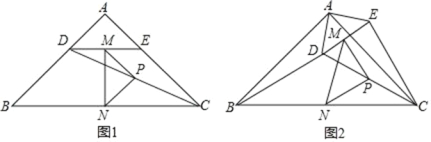
(3)分四种情况:
①如图,当![]() 在
在![]() 上且
上且![]() 时,
时,

![]() ,而
,而![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,即
的中点,即![]() ,
,
![]() ;
;
②如图,当![]() 在
在![]() 上且
上且![]() 时,
时,
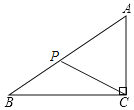
![]() ;
;
③如图,当![]() 在
在![]() 上且
上且![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
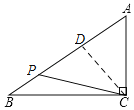
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() ;
;
④如图,当![]() 在
在![]() 上且
上且![]() 时,
时,![]() ,
,
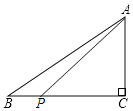
![]() .
.
综上所述,当![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
相关题目