题目内容
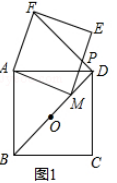
【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
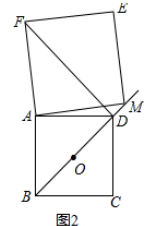
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
【答案】
(1)
解:BM=DF,BM⊥DF.
理由:∵四边形ABCD、AMEF是正方形,
∴AF=AM,AD=AB,∠FAM=∠DAB=90°,
∴∠FAM﹣∠DAM=∠DAB﹣∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
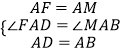 ,
,
∴△FAD≌△MAB,
∴BM=DF,∠FDA=∠ABD=45°,
∵∠ADB=45°,
∴∠FDB=45°+45°=90°,
∴BM⊥DF,
即BM=DF,BM⊥DF
(2)
解:BM=DF,BM⊥DF都成立,
理由是:∵四边形ABCD和AMEF均为正方形,
∴AB=AD,AM=AF,∠BAD=∠MAF=90°,
∴∠FAM+∠DAM=∠DAB+∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
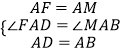 ,
,
∴△FAD≌△MAB,
∴BM=DF,∠ABM=∠ADF,
由正方形ABCD知,∠ABM=∠ADB=45°,
∴∠BDF=∠ADB+∠ADF=90°,
即BM⊥DF,
∴(1)中的结论仍成立
【解析】(1)根据正方形性质求出AF=AM,AD=AB,∠FAM=∠DAB=90°,推出∠FAD=∠MAB,证△FAD≌△MAB,推出BM=DF,∠FDA=∠ABD=45°,求出∠ADB=45°即可;(2)与(1)类似,根据正方形性质,推出∠FAD=∠MAB,判定△FAD≌△MAB,推出BM=DF,∠FDA=∠ABD=45°,求出∠ADB=45°即可.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱进价和售价如下表所示:
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 55 | 36 |
售价(元/箱) | 63 | 42 |
设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价﹣总进价).
(1)求总利润w关于x的函数关系式;
(2)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.