题目内容
已知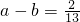 ,
,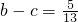 ,a2+b2+c2=1,求ab+bc+ca的值.
,a2+b2+c2=1,求ab+bc+ca的值.
解: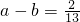 ,①
,①
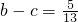 ,②
,②
由①+②,得
a-c=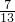 ,③
,③
∵(a-b)2+(b-c)2+(a-c)2=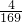 +
+ +
+ =
= ,
,
∴2(a2+b2+c2)-2(ab+bc+ca)= ,
,
∵a2+b2+c2=1,
∴2-2(ab+bc+ca)= ,
,
∴ab+bc+ca= .
.
分析:根据已知条件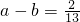 ,
,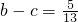 ,求得a-c=
,求得a-c=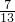 ;然后由(a-b)2+(b-c)2+(a-c)2=2(a2+b2+c2)-2(ab+bc+ca),求ab+bc+ca的值.
;然后由(a-b)2+(b-c)2+(a-c)2=2(a2+b2+c2)-2(ab+bc+ca),求ab+bc+ca的值.
点评:本题考查了完全平方公式,巧妙地用到了完全平方公式,把已知条件转化为三个完全平方式,然后将a2+b2+c2=1整体代入求值即可.
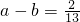 ,①
,①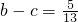 ,②
,②由①+②,得
a-c=
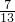 ,③
,③∵(a-b)2+(b-c)2+(a-c)2=
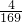 +
+ +
+ =
= ,
,∴2(a2+b2+c2)-2(ab+bc+ca)=
 ,
,∵a2+b2+c2=1,
∴2-2(ab+bc+ca)=
 ,
,∴ab+bc+ca=
 .
.分析:根据已知条件
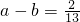 ,
,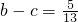 ,求得a-c=
,求得a-c=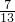 ;然后由(a-b)2+(b-c)2+(a-c)2=2(a2+b2+c2)-2(ab+bc+ca),求ab+bc+ca的值.
;然后由(a-b)2+(b-c)2+(a-c)2=2(a2+b2+c2)-2(ab+bc+ca),求ab+bc+ca的值.点评:本题考查了完全平方公式,巧妙地用到了完全平方公式,把已知条件转化为三个完全平方式,然后将a2+b2+c2=1整体代入求值即可.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
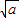 +
+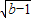 =
= ,则a2+b2的平方根是 .
,则a2+b2的平方根是 .