��Ŀ����
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB��90����AC��BC��6��D���߶�BC�ϣ�E���߶�AD��һ�㣮����CEΪֱ�DZߣ�CΪֱ�Ƕ��㣬��CE���·�������ֱ����ECF������BF��
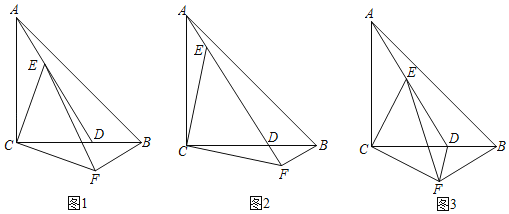
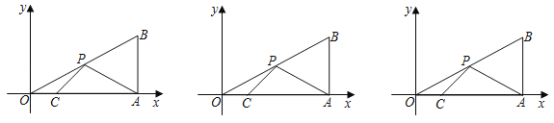
��1����ͼ1����֤��AE��BF��
��2����A��E��F���㹲��ʱ����ͼ2����BF��2����AF�ij���
��3����ͼ3������BAD��15��������DF����E�˶���ʹ�á�ACE��30��ʱ������DEF�������
���𰸡���1������������2��AF��2![]() ����3��S��EDF��3
����3��S��EDF��3![]() ��3��
��3��
��������
��1����ͼ1�У�֤����ACE�ա�BCF��SAS�����ɽ�����⣻
��2������ȫ�������ε����ʣ�֤����ACD=��DFB=90���������ù��ɶ������ɽ�����⣻
��3����ͼ3�У���FH��BC��H��֤����BCF�ǵ�Ϊ30���ĵ��������Σ����CF��FB��FH������S��EDF=S��ECD+S��CDF-S��ECF���㼴�ɣ�
��1��֤������ͼ1�У�
�ߡ�ACB����ECF���ǵ��������Σ�
��CA��CB��CE��CF����ACB����ECF��90����
���ACE����BCF��
���ACE�ա�BCF��SAS����
��AE��BF��
��2����ͼ2�У�
��CA��CB��6����ACB��90����
��AB��6![]() ��
��
�ߡ�ACE�ա�BCF��
���CAD����DBF��
�ߡ�ADC����BDF��
���ACD����DFB��90����
��AF��![]() ��
��![]() ��2
��2![]() ��
��
��3����ͼ3�У���FH��BC��H��
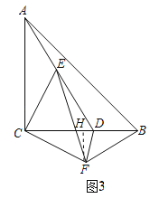
�ߡ�ACE����CAE��30����
��AE��EC��
�ߡ�ACE�ա�BCF��
��BF��AE��CF��CE��
��CF��BF����FCB����CBF��30����
��FC��FB��FH��BC��
��CH��BH��3��FH��![]() ��CF��BF��2
��CF��BF��2![]() ��
��
�ߡ�CED����CAE+��ACE��60������ECD��90����30����60����
���ECD�ǵȱ������Σ�
��EC��CF��CD��2![]() ��
��
��S��EDF��S��ECD+S��CDF��S��ECF��![]() ����2
����2![]() ��2+
��2+![]() ��2
��2![]() ��
��![]() ��
��![]() ��2
��2![]() ��2
��2![]() ��3
��3![]() ��3��
��3��