Question

【题目】梯形ABCD中AB∥CD，∠ADC＋∠BCD＝90°，以AD、AB、BC为斜边向形外作等腰直角三角形，其面积分别是，且，则CD＝（ ）

A.2.5ABB.3ABC.3.5ABD.4AB

Answer 1

【答案】B

【解析】

分别用斜边AD、AB、BC把S1、S2、S3表示出来，然后根据S1+S3=4S2求出AD、AB、BC之间的关系．在过点B作BK∥AD交CD于点K后，根据数据发现△KBC又是一个直角三角形，再次利用勾股定理即可发现CD和AB之间的关系．

解：∵以AD、AB、BC为斜边向外作等腰直角三角形，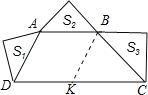

其面积分别是S1、S2、S3，
∴，， ,

∵S1+S3=4S2，
∴AD2+BC2=4AB2
过点B作BK∥AD交CD于点K，
∵AB∥CD
∴AB=DK，AD=BK，∠BKC=∠ADC
∵∠ADC+∠BCD=90°
∴∠BKC+∠BCD=90°
∴BK2+BC2=CK2
∴AD2+BC2=CK2
∴CK2=4AB2
∴CK=2AB
∴CD=3AB．

故选：B.