题目内容
如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠无缝隙），求长方形的面积．
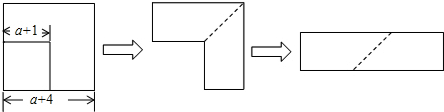
分析：利用大正方形的面积减去小正方形的面积即可，解题时注意完全平方公式的运用．
解答：解：矩形的面积为：
（a+4）2-（a+1）2
=（a2+8a+16）-（a2+2a+1）
=a2+8a+16-a2-2a-1
=6a+15．
答：长方形的面积是（6a+15）cm2．
（a+4）2-（a+1）2
=（a2+8a+16）-（a2+2a+1）
=a2+8a+16-a2-2a-1
=6a+15．
答：长方形的面积是（6a+15）cm2．
点评：此题考查了图形的剪拼，关键是根据题意列出式子，运用完全平方公式进行计算，要熟记公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10、如图，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为（ ）
