题目内容
【题目】某景区一电瓶小客车接到任务从景区大门出发，向东走2千米到达A景区，继续向东走2.5千米到达B景区，然后又回头向西走8.5千米到达C景区，最后回到景区大门.
（1）以景区大门为原点，向东为正方向，以1个单位长表示1千米，建立如图所示的数轴，请在数轴上表示出上述A、B、C三个景区的位置.
（2）A景区与C景区之间的距离是多少？
（3）若电瓶车充足一次电能行走15千米，则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务？请计算说明.
【答案】(1)、答案见解析；(2)、6千米；(3)、不能
【解析】
试题分析：(1)、向东为正，向西为负，然后根据所行走的路程得出点的坐标；(2)、两点之间的距离为两点所表示的数的差的绝对值；(3)、首先根据绝对值的性质得出所走的路程之和，然后与15进行比较大小.
试题解析：(1)、如图，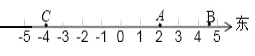
(2)、A景区与C景区之间的距离是：2－(－4)=6(千米)
(3)、不能完成此次任务
电瓶车一共走的路程为：|+2|+|2.5|+|﹣8.5|+|+4|=17（千米），
因为17＞15 所以不能完成此次任务．
练习册系列答案
同步练习强化拓展系列答案
相关题目
