Question

如图：在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上。 正确的是     （填序号）

 

Answer 1

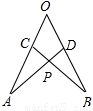
【答案】

①②③

【解析】

试题分析：根据题中条件，由两边夹一角可得△AOD≌△BOC，得出对应角相等，又由已知得出AC=BD，可得△APC≌△BPD，同理连接OP，可证△AOP≌△BOP，进而可得出结论．

∵OA=OB，OC=OD，∠O为公共角，

∴△AOD≌△BOC，

∴∠A=∠B，

又∠APC=∠BPD，

∴∠ACP=∠BDP，

OA-OC=OB-OD，即AC=BD，

∴△APC≌△BPD，

∴AP=BP，

连接OP，

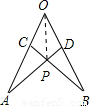
即可得△AOP≌△BOP，得出∠AOP=∠BOP，

∴点P在∠AOB的平分线上．

故题中结论都正确．

故答案为：①②③．

考点：本题考查的是三角形全等的判定方法

点评：解答本题的关键是熟练掌握判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA和HL，做题时，要根据已知条件结合图形进行思考．