题目内容
已知:梯形ABCD中,AD∥BC,∠ABC=90°,AD=12,BC=18,AB=a,点P是线段BC上的自C向B运 动的一动点,移动的速度是1厘米/秒,连接DP,作射线PE垂直于PD,PE与直线AB交于点E.
动的一动点,移动的速度是1厘米/秒,连接DP,作射线PE垂直于PD,PE与直线AB交于点E.
(1)确定CP=6时,点E的位置;
(2)若设运动时间为x秒,BE=y,求y关于x的函数关系式,并指出自变量x的取植范围;
(3)是否能在线段BC上找到不同的两个点P1,P2,使得上述作法得到的点E与点A重合?若存在,求a的取值范围;若不存在,请说明理由.
解:(1)当CP=6时,DP⊥BC,又∠DPE=90°,
∴E与B重合;
(2)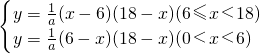 ;
;
(3)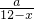 =
= ,a2=12x-x2
,a2=12x-x2
x2-12x+a2=0
法1:△=144-4a2>0,a2<36
∵a>0,∴a<6
方法2:a2=(x2-12x)=-(x2-12x+36)+36
=-(x-6)2+36<36
∴a<6
∵a>0
∴0<a<6.
分析:本题属于分段函数,x=6时,B、E重合,以x=6为分界点,把函数分成两段求,过D点作BC边上的高,利用相似三角形的性质解.
点评:P为BC上的动点,点在动,不管点E在线段AB上,还是线段AB外,相似关系却没有变.
∴E与B重合;
(2)
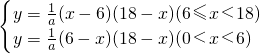 ;
;(3)
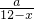 =
= ,a2=12x-x2
,a2=12x-x2x2-12x+a2=0
法1:△=144-4a2>0,a2<36
∵a>0,∴a<6
方法2:a2=(x2-12x)=-(x2-12x+36)+36
=-(x-6)2+36<36
∴a<6
∵a>0
∴0<a<6.
分析:本题属于分段函数,x=6时,B、E重合,以x=6为分界点,把函数分成两段求,过D点作BC边上的高,利用相似三角形的性质解.
点评:P为BC上的动点,点在动,不管点E在线段AB上,还是线段AB外,相似关系却没有变.

练习册系列答案
相关题目
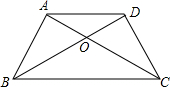 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明. 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( ) 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )