题目内容
【题目】如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD= ![]() BC.
BC. 
(1)用尺规作图的方法,过E点作EF⊥DC,垂足是点F;(不写作法,保留作图痕迹)
(2)求证:DF=CF.
【答案】
(1)解:如图,EF即为所求;
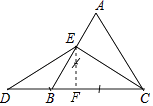
(2)证明:∵△ABC是等边三角形,点E是AB的中点,
∴CE⊥AB,BE= ![]() AB,∠ABC=60°,
AB,∠ABC=60°,
∵BD= ![]() BC,
BC,
∴BD=BE,
∴∠D=∠BED=30°.
在Rt△BCE中,
∵∠CEB=90°,∠ABC=60°,
∴∠BCE=30°,
∴DE=CE.
【解析】(1)过点E作EF⊥BC于点F即可;(2)根据等边三角形的性质得出CE⊥AB,BE= ![]() AB,再由BD=
AB,再由BD= ![]() BC可得出BD=BE,故可得出∠D=30°,在Rt△BCE中可得出∠BCE=30°,故可得出结论.
BC可得出BD=BE,故可得出∠D=30°,在Rt△BCE中可得出∠BCE=30°,故可得出结论.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目